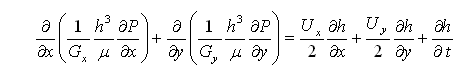
See also: Full DyRoBeS©_BePerf Manual
DyRoBeS©_BePerf computer program has been developed to analyze the Bearing steady state and dynamic Performance of fixed lobe, flexural pad, and tilting pad hydrodynamic journal bearings based on Finite Element Analysis (FEA). In addition to bearing analysis, the program also performs lubricant properties analysis and oil flow calculation. The acronym, DyRoBeS©, denotes Dynamics of Rotor Bearing Systems.
The governing equation for pressure distribution in a fluid film journal bearing is incompressible Reynolds equation which is derived from the Navier-Stokes equation, as expressed below. The fluid film forces acting on the journal are determined by application of boundary conditions and integration of pressure distribution. It is an iterative process until the convergence criterion is satisfied. Once the static equilibrium is found, the bearing static performance, such as bearing eccentricity ratio, attitude angle, minimum film thickness, maximum film pressure, frictional power loss, oil flow rate, etc., can be easily determined. Under dynamic conditions, the journal is oscillating with small amplitudes around the static equilibrium position. The eight bearing dynamic coefficients (stiffness and damping) are obtained by solving the perturbed pressure equations.
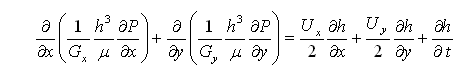
where x is in the axial direction and y is in the circumferential direction. Gx and Gy called the turbulent flow coefficients are the correctional terms of viscosity caused by the turbulent diffusion:
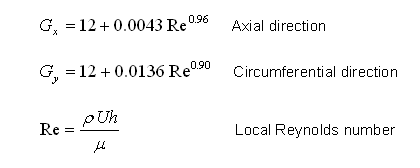
For laminar flow, Gx = Gy = 12. A critical parameter affected by turbulence is the shear stress acting on the shaft.
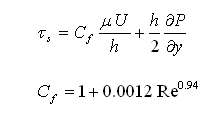
where Cf is the turbulent Couette shear stress factor. For laminar flow, Cf = 1.
The boundary conditions in the axial coordinate are that the pressure is ambient at the edges of the bearing pad. The Swift-Stieber or Reynolds boundary conditions are applied in the circumferential coordinate. Film cavitation is considered and the transition boundary curve to the film rupture is determined by iteration.
The governing equation for pressure distribution in a gas/air lubricated journal bearing is compressible Reynolds equation.
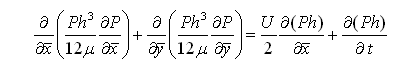
This compressible Reynolds equation is more difficult to analyze due to the existence of the pressure (P) in each terms compared with the incompressible flow, which makes the problem non-linear. Weak formulation based on variational principle is applied for generating the finite element model for the boundary value problems. Since this is a nonlinear problem, Newton-Raphson’s iterative scheme is utilized to solve the pressure increment, or pressure correction.
The solutions techniques for the incompressible and compressible Reynolds equation are discussed in the book – Introduction to Dynamics of Rotor-Bearing Systems by W. J. Chen and E. J. Gunter, 2005.
The DyRoBeS© Bearing program consists of seven primary modules:
See also: Full DyRoBeS©_BePerf Manual
Copyright © 2014-2017