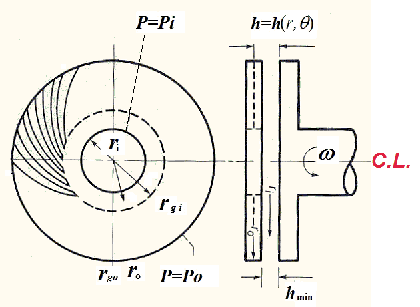
Seal Geometry & Boundary Conditions

Seal Geometry & Boundary Conditions

A typical inward pumping spiral groove seal with a constant groove depth is shown below:

Pressures are specified at Seal Inner Diameter and Outer Diameter boundaries.

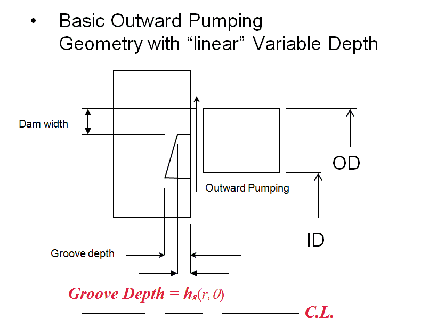
·Constant Groove Depth,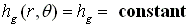

·Variable Groove Depth,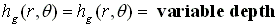

Groove depth can be varying with (r,). Groove depth only causes the addition film thickness in the GROOVE area, not in the land area.

Coning, e, addition film thickness 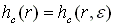, e is a constant given value

Additional film thickness can be caused by surface coning in the entire area. Regardless the inward or outward pumping, a POSITIVE coning is defined such that the film thickness DECREASES with radius. A negative coning will have film thickness INCREASES with radius. Therefore, for a positive coning, the minimum film thickness occurs at the SEAL OD, and a negative coning will have the minimum film thickness at SEAL ID.

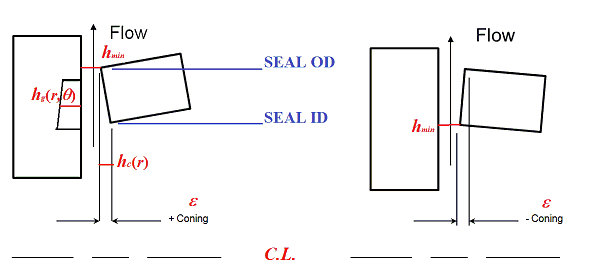
if e > 0, hmin at SEAL OD

The additional film thickness over the entire domain due to coning is:

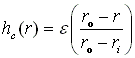
Check both boundaries:

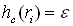
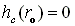
if e < 0, hmin at SEAL ID

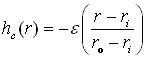
Check both ends:

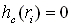
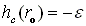(note that this is a positive number since e is a negative number)

Therefore, the film thickness in Reynolds Eq. (1) becomes:

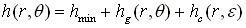
hmin is the minimum film thickness which is a constant and is given in the input.

hg is the groove depth and additional film thickness in the groove area only.

hc is the additional film thickness in the entire domain due to coning.

Other geometry definitions for SPIRAL groove seal are shown below.

ri = Seal Face inner radius = SEAL ID/2

ro = Seal Face outer radius = SEAL OD/2

rgi = Groove inner radius = GROOVE ID/2

rgo = Groove outer radius = GROOVE OD/2

dw = Dam width

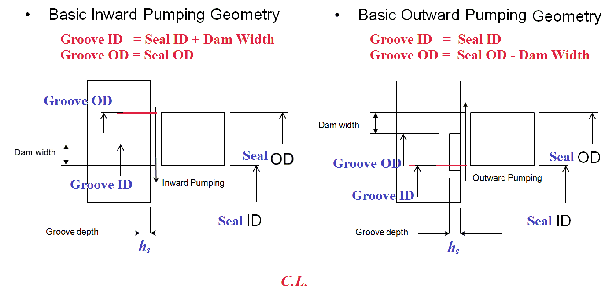
For inward pumping SPIRAL GROOVE seal

rgi = ri + dw = SEAL INNER RADIUS + Dam Width

rgo = ro

For outward pumping SPIRAL GROOVE seal

rgi = ri

rgo = ro - dw = SEAL OUTER RADIUS - Dam Width

Note that for SPIRAL Groove seal, the groove inner and outer radii are constant due to constant dam width. However, for the OBLIQUE Groove seal, the corner points are connected by straight lines, then the groove inner radius is NOT constant for inward pumping and groove outer radius is NOT constant for outward pumping. Check the dam width to be sure that the straight lines are within the seal domain.

Ng = # of spirals

g = Groove width at groove inner radius (width between two spiral curves in circumferential direction)

L = Land width at groove inner radius (width between grooves in circumferential direction)

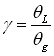Land/Groove Ratio

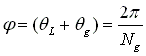One pitch

The spiral line is defined as

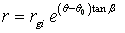
where is the spiral angle measured at the beginning of the spiral (at rgi ), o is the spiral starting angle at 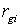. Or if r is know, the theta is:

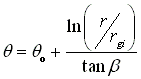
To illustrate the boundaries and solution domain, a 4 general grooves (or pockets) design is sketched below:

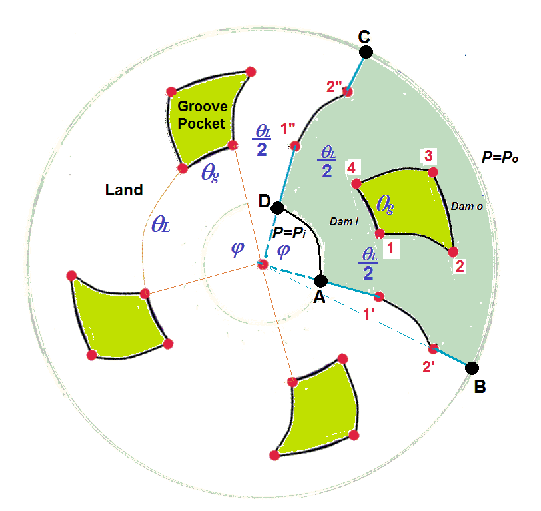
Points (1,2,3,4) form a pocket or groove.

Points (A,B,C,D) form a pitch (sector), if a sector is analyzed.

Curve AD has the same radius, ri = Seal ID/2. Pressure is specified as Pi on curve AD.

Curve BC has the same radius, ro = Seal OD/2. Pressure is specified as Po on curve BC.

For inward pumping, Dam o = 0, curve 23 are on the boundary curve BC.

For outward pumping, Dam i = 0, curve 14 are on the boundary curve AD.

Curves 12 and 43 are spiral curves for spiral groove and straight lines for oblique groove.

Curve 1'2' on the boundary curve AB is obtained by rotating curve 12 with half of the land width CW. i.e. .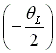

Curve 1"2" on the boundary curve DC is obtained by rotating curve 12 with groove width + half of the land width CCW. i.e. .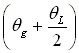

Coordinates for the 8 boundary points:

1: (r1, 1) = (rgi, 1) rgi = ri + Dam i

2: (r2, 2) = (rgo, 2) rgo = ro - Dam o

3: (r3, 3) = (rgo, 3)

4: (r4, 4) = (rgi, 4)

A: (rA, A) = (ri, A)

B: (rB, B) = (ro, B)

C: (rC, C) = (ro, C)

D: (rD, D) = (ri, D)

The radius coordinates are known now and the angular coordinates are all related. Assuming 1 is known, it can be any arbitrary number without affecting results. Let b1 and b2 be the spiral angles for curves 12 and 43.

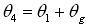
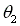is determined by Eq. (g), 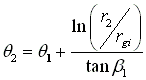, where r2, rgi, 1, and b1 are known.

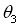is determined by Eq. (g), 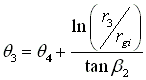, where r3, rgi, 4, and b2 are known.

Note: if spiral angle b= 90o, the spiral line becomes a radial line with constant theta.

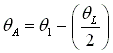
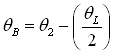
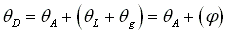
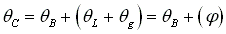
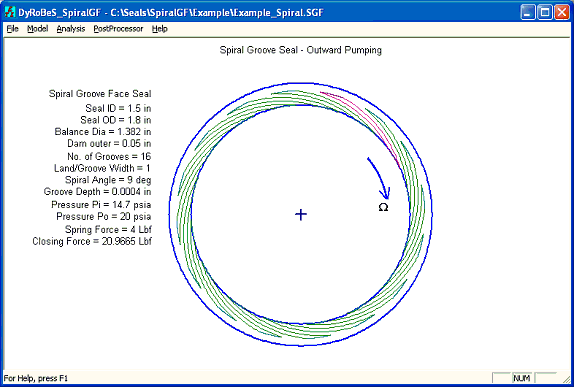
Spiral Groove Seal

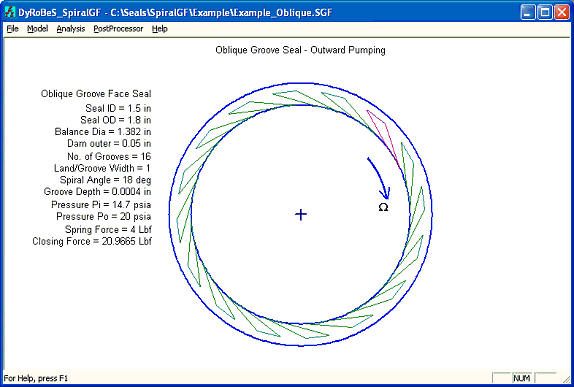
Oblique Groove Seal