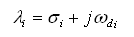
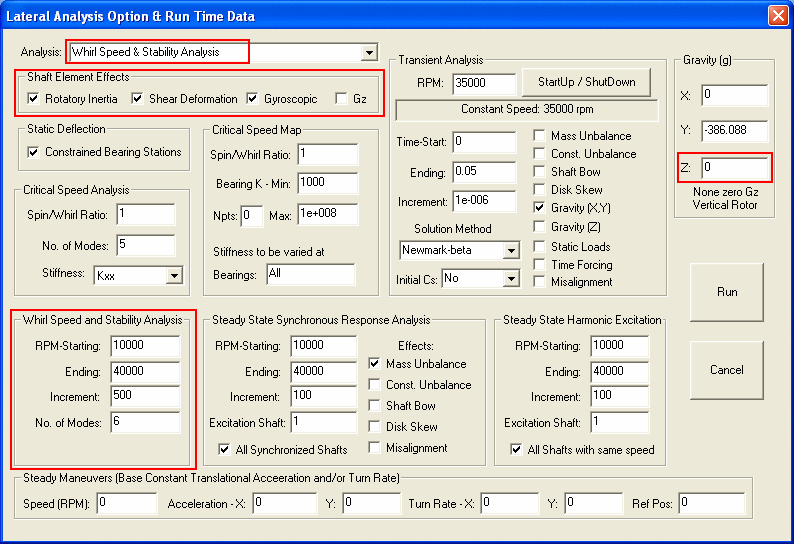
Whirl Speed and Stability Analysis
The Whirl Speed and Stability Analysis calculates the damped natural frequencies (whirl speeds), damping coefficients, logarithmic decrements, damping factors, and precessional mode shapes. The QR algorithm is utilized in the calculation of eigenvalues and eigenvectors. This algorithm has been well proven to be reliable and numerically stable. The imaginary parts of the eigenvalues are the system damped natural frequencies and they can be used to determine the damped critical speeds. The real parts of the eigenvalues are the system damping coefficients which can be used to determine the system stability. A positive damping coefficient indicates system instability. Very often, the logarithmic decrements or damping factors are used to determine the system stability. A negative logarithmic decrement or damping factor indicates system instability. When the value of a logarithmic decrement exceeds 1, that particular mode is considered to be well damped. Due to the non-symmetric properties of the bearing coefficients and the gyroscopic effect, the Whirl Speed Map and Stability Map are very complex in nature, caution must be taken when preparing these maps.
The run time data required in this analysis are shaft rotational speeds (starting, ending, and incremental speeds) and number of modes. For multiple shaft systems, the shaft speed is referred to the shaft number 1 speed. For single speed calculation, enter the speed as the starting speed and set the ending speed and incremental speed to zero. The number of modes is used to specify the number of precessional modes that mode shapes (eigenvectors) are calculated for. The value of zero indicates that only the eigenvalues are calculated and no mode shapes (eigenvectors) are calculated. Generally, only the lowest 4 to 6 precessional modes are of importance in practice. More modes are required for large systems.
A complex eigenvalue is given by:
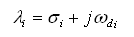
where the subscript I is the mode number. If the damped natural frequency is a non-zero value, this mode is a precessional mode with an oscillating frequency equals to the damped natural frequency. If the damped natural frequency equals to zero, this mode is a real mode (pure rigid body mode) or non-oscillating mode. The logarithmic decrement and damping factor of a precessional mode are defined to be:

The logarithmic decrement is commonly used in the lateral vibration and damping factor is commonly referred in the torsional analysis.
For sample outputs, click Whirl Speed and Stability Maps.
Copyright © 2014-2017